📋 Elke oefentoets bestaat uit 10 meerkeuzevragen, willekeurig gekozen uit een database met tientallen vragen. Hierdoor kun je dezelfde test meerdere keren doen zonder exact dezelfde vragen te krijgen – perfect om te blijven oefenen
Dit gaat niet om snelheid, maar om nadenken 🧠.
Is de som lastig? Mooi zo 👍. Pak papier en potlood ✏️… en werk stap voor stap.
Geen haast 🐢. Er is geen stopwatch ⏱️ en je wint geen medaille 🥇 voor snelheid.
Doe het goed, niet snel.
Rekenen win je met je hoofd, niet met haast 💪.
Resultaten
Top gedaan, leesexpert! 📚🌟
Je hebt laten zien dat je begrijpend lezen goed onder de knie hebt. Je inzet en doorzettingsvermogen werpen hun vruchten af. Klaar voor een nieuwe uitdaging?
- Signaalwoorden speuren – Let tijdens het lezen op woorden als ‘omdat’, ‘maar’ en ‘daarom’. Ze helpen je de structuur van de tekst te begrijpen.
- Samenvatten – Probeer na het lezen van elke alinea in één zin samen te vatten wat je hebt gelezen.
- Vragen stellen – Stel jezelf tijdens het lezen vragen zoals ‘Wat bedoelt de schrijver hiermee?’ of ‘Waarom gebeurt dit?’
Onthoud: «Lezen is de sleutel tot kennis.» Blijf zo doorgaan! 🚀
🧐 Bericht voor leerlingen met minder dan 70% goed
Geen zorgen, dappere lezer! 🌱
Begrijpend lezen kan soms lastig zijn, maar elke dag biedt een nieuwe kans om te groeien. Probeer deze tips:
- Voorspellen – Kijk naar de titel en afbeeldingen van de tekst en probeer te voorspellen waar het over gaat.
- Visualiseren – Maak in je hoofd een beeld van wat je leest. Dit helpt je de tekst beter te begrijpen.
- Woordenboek gebruiken – Kom je een moeilijk woord tegen? Zoek het op en schrijf het op in je eigen woordenboek.
Onthoud: «Elke expert was ooit een beginner.» Blijf oefenen, en je zult merken dat het steeds beter gaat! 💪📖
Maak je geen zorgen, rekenheld in wording! 🌟✏️
Rekenen kan soms best lastig zijn, maar met oefenen ga je vooruit. Probeer deze tips:
- Stap voor stap – Breek sommen in kleinere stukjes. Zo worden moeilijke sommen makkelijker te begrijpen.
- Gebruik schema’s – Teken een schema of diagram bij lastige verhaalsommen. Dit maakt het probleem duidelijker.
- Herhaal basisvaardigheden – Oefen regelmatig tafels, breuken en procenten. Een goede basis maakt rekenen makkelijker.
Onthoud: «Iedere meester was ooit een leerling.» Blijf oefenen, dan lukt het steeds beter! 💪📈
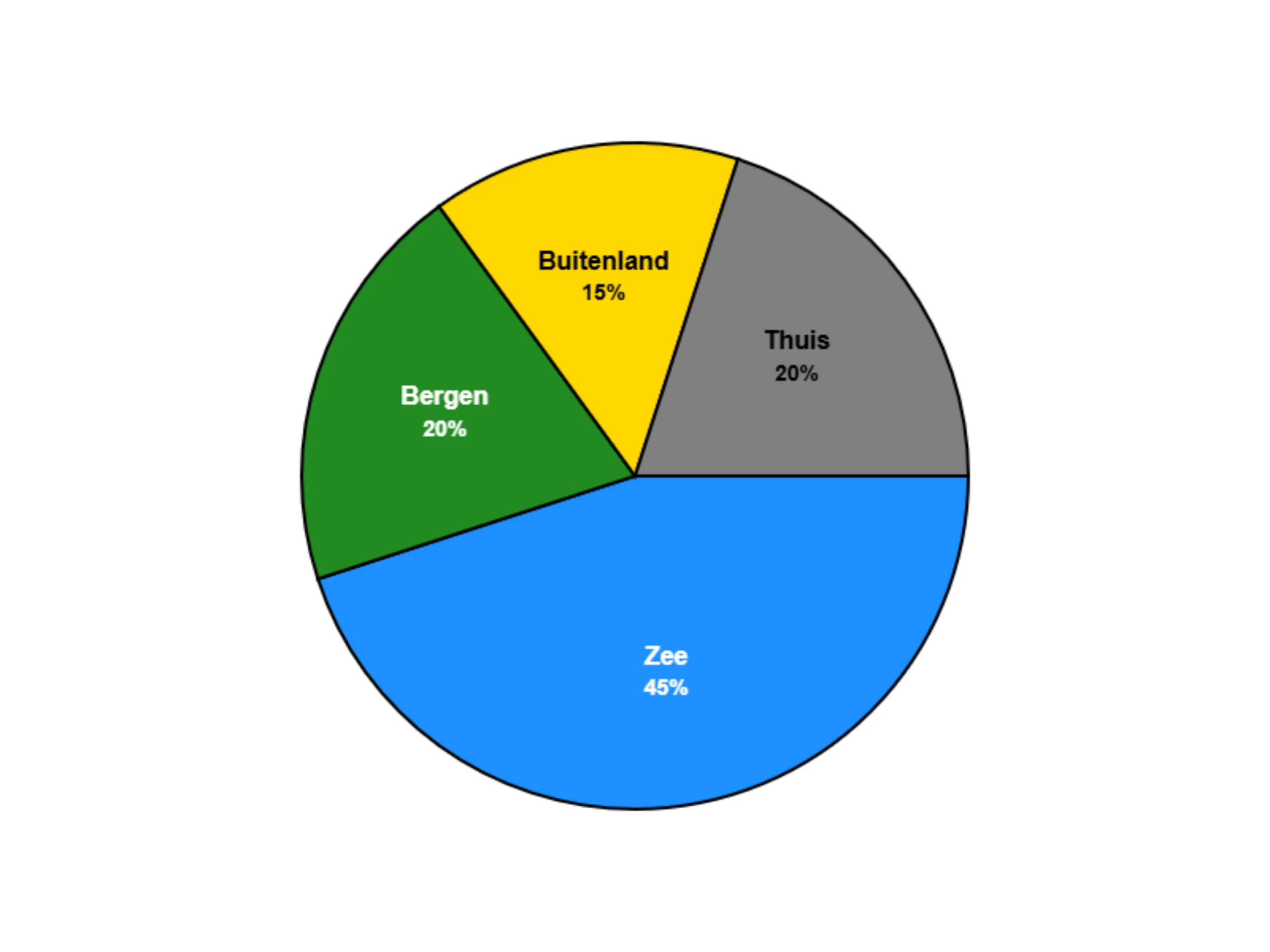
#1. Hoeveel meer leerlingen gaan naar zee dan naar het buitenland bij 120 leerlingen totaal?

#2. Als 120 leerlingen vakantie vieren en 20% thuisblijft, hoeveel leerlingen is dat?
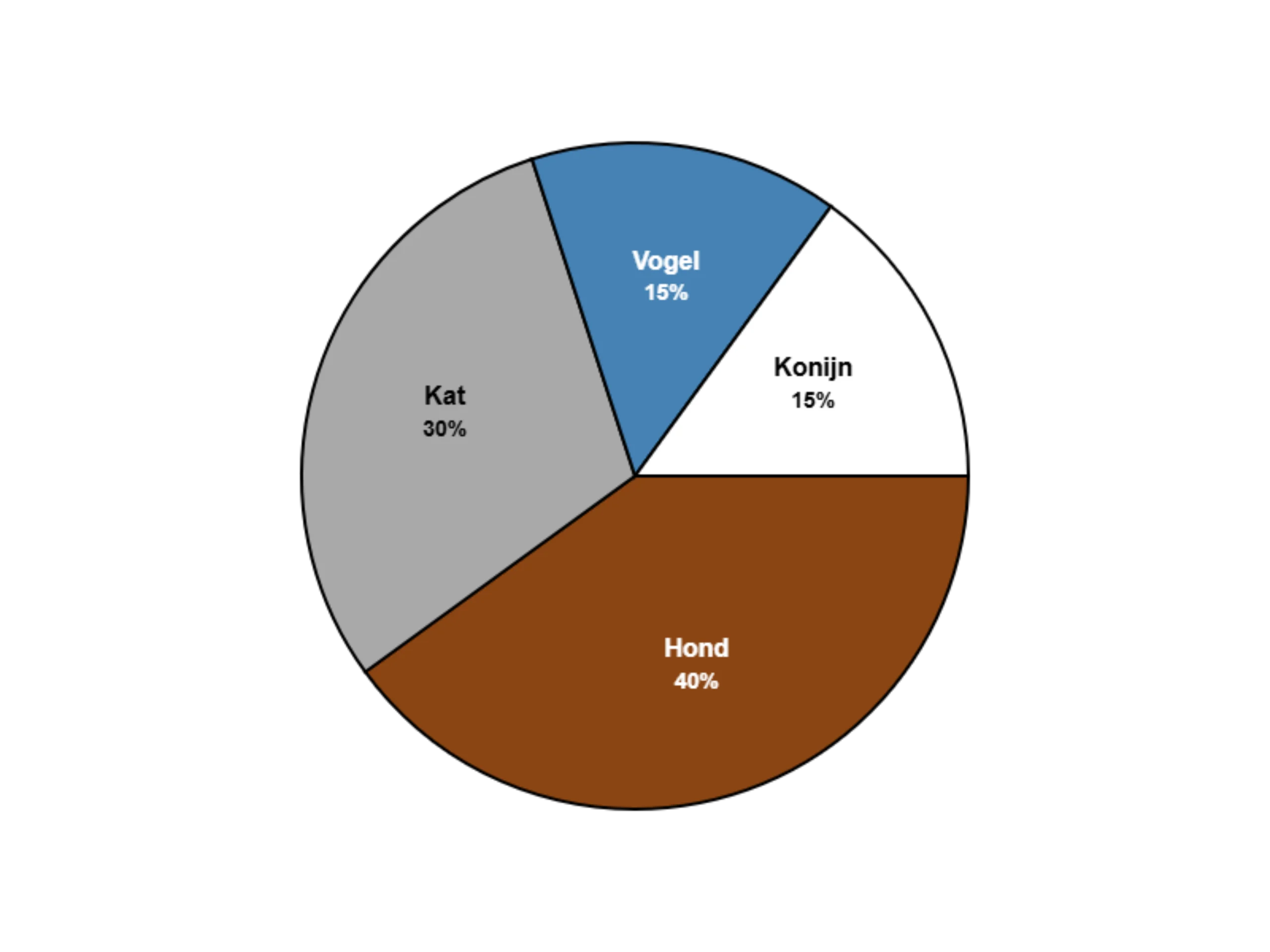
#3. Hoeveel leerlingen hebben samen een kat of vogel bij 60 leerlingen totaal?
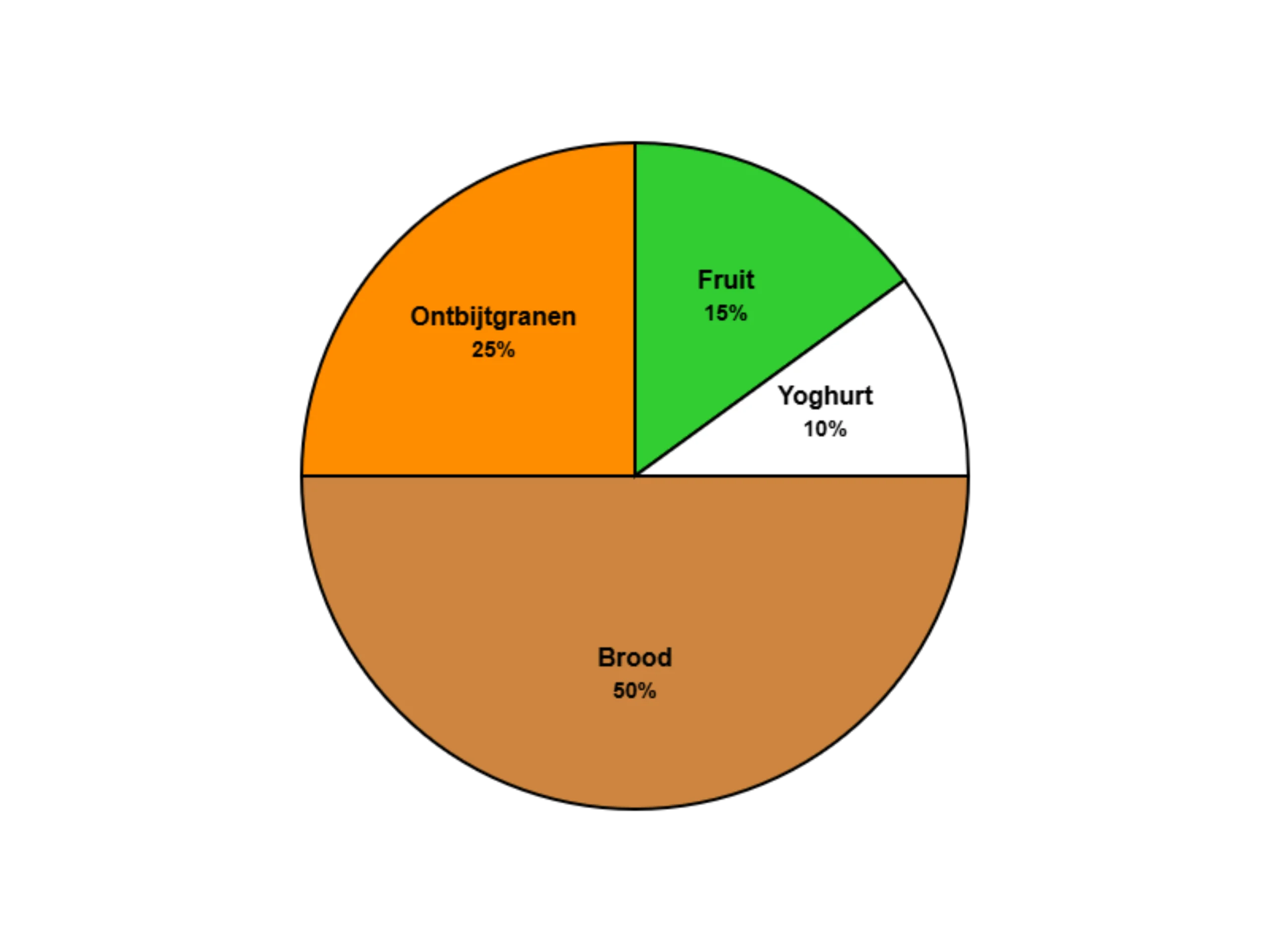
#4. Als 200 kinderen ontbijten en 25% eet ontbijtgranen, hoeveel kinderen is dat?

#5. Het cirkeldiagram over vakanties toont dat 45% naar zee gaat. Welke breuk is dit?

#6. Het diagram toont zee (45%), bergen (20%), buitenland (15%) en thuis (20%). Klopt dit totaal?
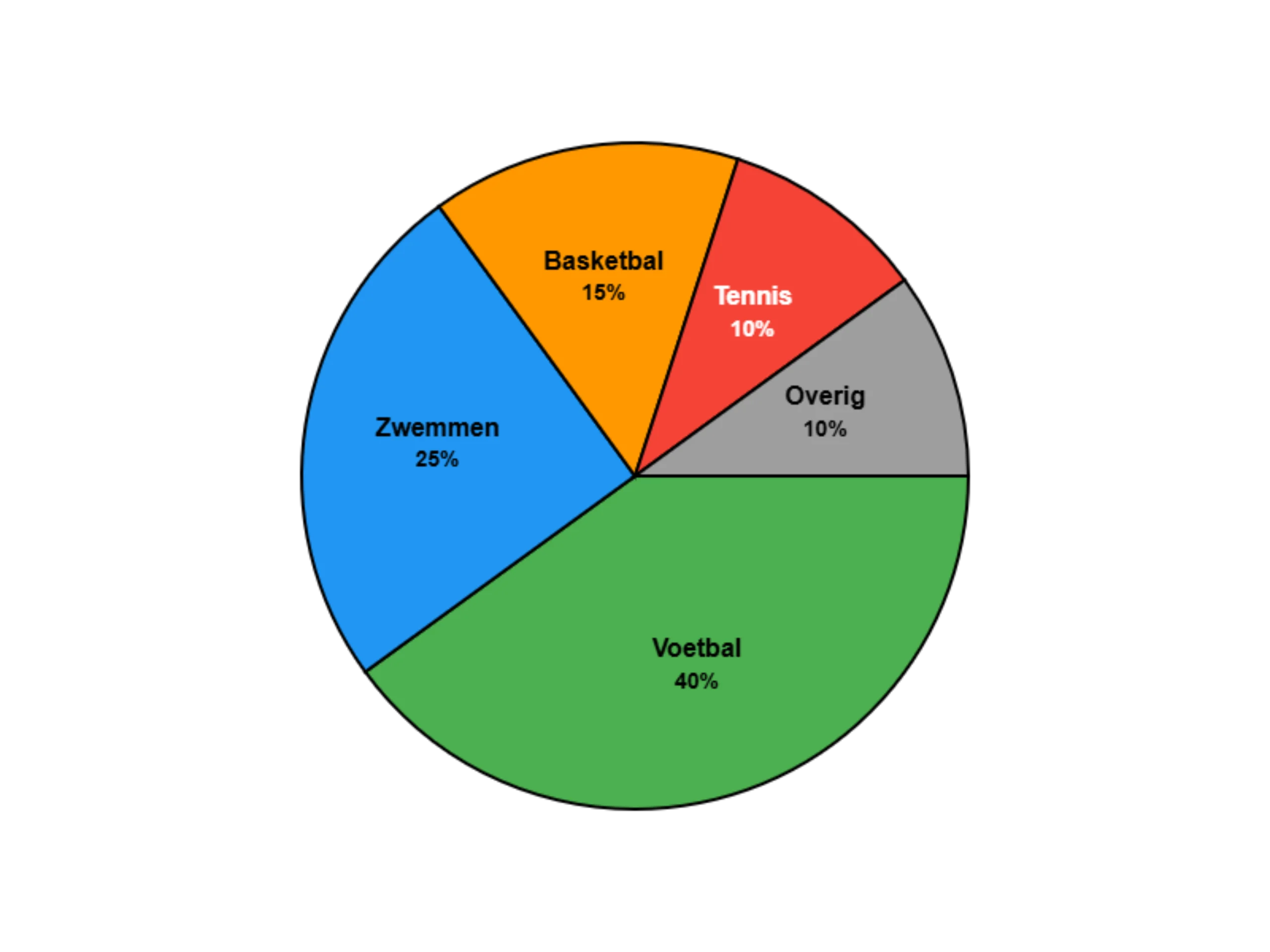
#7. Tennis heeft 10% in het diagram. Hoeveel leerlingen is dat bij een totaal van 80?

#8. Volgens het vakantiediagram gaat 20% naar de bergen en 15% naar het buitenland. Hoeveel procent samen?

#9. Het cirkeldiagram over huisdieren toont dat honden 40% uitmaken. Bij 60 leerlingen, hoeveel hebben een hond?







